티스토리 뷰
문제
"이진 트리의 루트와 정수 targetSum이 주어졌을 때, 경로를 따라 값들의 합이 targetSum과 같은 경로의 수를 반환하세요.경로는 반드시 루트에서 시작하거나 잎 노드에서 끝날 필요는 없지만, 반드시 아래 방향으로 진행해야 합니다 (즉, 부모 노드에서 자식 노드로만 이동해야 합니다)."이 문제는 다음과 같은 특징을 가집니다:
- 경로의 시작점이 반드시 루트일 필요는 없습니다.
- 경로의 끝점이 반드시 잎 노드일 필요는 없습니다.
- 경로는 반드시 위에서 아래로 진행해야 합니다 (부모에서 자식으로).
- 목표는 주어진 targetSum과 일치하는 경로의 총 개수를 찾는 것입니다.
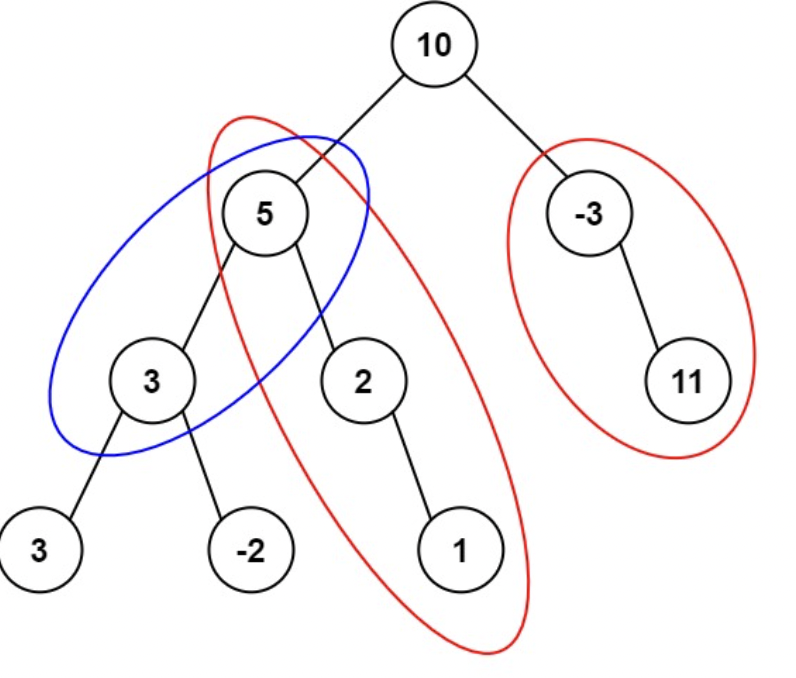
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.
위 문제는 그래프가 주어졌을 때 한 노드 기준으로 아래 방향으로 더함을 진행할 때 특정 targetSum값을 만족하는 개수를 구하는 문제입니다.
흔히 착각할 수 있는 것이 Root 노드를 기준으로 계산하면 되겠지라고 할 수 있겠지만, 여기서 생각해야할 부분은 Root점만이 시작점이 아니고 어느 노드든지 시작점이 되어 계산이 될 수 있어야한다는 점입니다.
해당 문제는 DFS문제로서 재귀함수를 통해 처리할 수 있습니다. 재귀함수를 통해 처리할 수 있는 이유는 같은 계산이 반복적으로 이루어지는 구조이기 때문에 재귀함수를 통해 계산할 수 있습니다.
알고리즘 코드를 통해 알아보겠습니다.
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if(root == null)
return 0;
return checkPathSum(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
}
public int checkPathSum(TreeNode root, int targetSum) {
if(root == null)
return 0;
targetSum -= root.val;
int count = targetSum == 0 ? 1 : 0;
count+= checkPathSum(root.left, targetSum);
count+= checkPathSum(root.right, targetSum);
return count;
}
}
checkPathSum은 targetSum에 대한 값의 일치를 확인하기 위한 메소드 입니다.
안에 내용을 보게 된다면 우선 해당 노드가 null일 경우에는 0을 반환합니다. 즉 더이상 확인할 노드가 존재하지 않는다는 의미이며, 내려갈 곳이 없다는 것을 알려줍니다.
targetSum -= root.val 부분은 우리가 확인해야 할 부분은 결국 targetSum 합과 동일한 경로를 찾아내야합니다. 반대로 targetSum을 대상으로 뺐을 때 결과가 0이 되는 시점이 해당 경로는 targetSum과 동일하다는 것을 알려주는 경우가 되겠습니다.
그렇기 때문에 위와 같이 targetSum 에서 root.val을 빼는 과정을 반복함으로서 그 결과가 0일 경우는 카운트를 아닌 경우는 0을 주어 카운트를 유지 시켜줍니다.
이 계산 하는 부분이 우리가 카운트를 구하기 위한 전부에 해당합니다.
이제 이러한 과정을 위 문제에서 얘기하다시피 아래 방향으로 쭉 내려가야하는 구조이기 때문에 checkPathSum 내에서 재귀함수를 주어 계산을 하도록 합니다. left와 right를 주어 처리하는 이유는 노드의 서브 트리가 양쪽으로 나눠지는 그래프이기 때문에 그렇습니다.
자 이제 우린 계산하는 메소드를 완성하였습니다. 이제 이 메소드를 적용하여 계산만 해주면 됩니다.
그러면 우린 이제 pathSum에다가 checkPathSum(root, targetSum) 하나만 선언해주면 될까요?
안됩니다. 하나만 선언하게 된다면 Root에 대한 결과만을 가져오게 될 것입니다. 그렇다면 이렇게 하는건 어떨까요?
public int pathSum(TreeNode root, int targetSum) {
if(root == null)
return 0;
return checkPathSum(root, targetSum) + checkPathSum(root.left, targetSum) + checkPathSum(root.right, targetSum);
}
위 코드는 Root 시작점과 Root에 연결된 서브 트리 왼쪽과 오른쪽을 계산하여 더해주는 작업을 하고 있습니다. 이렇게 되면 Root 시작점과 왼쪽 서브 노드 , 오른쪽 서브 노드를 다 확인하니 괜찮을까요??
이렇게 하기에는 뭔가 부족한면이 느껴집니다. 과연 그게 어떤걸까요?
이미 문제에서는 힌트를 주고 있었습니다. 빨간 글씨를 보겠습니다. -> 경로의 시작점이 반드시 루트일 필요는 없습니다. 즉, Root만을 확인해서는 안되고 모든 노드가 시작점이 될 수 있도록 해야한다, 곧 모든 노드를 확인하도록 해야한다.라는 의미를 가집니다.
위의 코드는 단순 Root와 left, right에 대한 노드만을 체크했습니다. 그렇기 때문에 제대로된 결과를 확인할 수 가 없습니다.
그렇기 때문에 아래와 같은 코드를 작성해야합니다.
public int pathSum(TreeNode root, int targetSum) {
if(root == null)
return 0;
return checkPathSum(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
}
checkPathSum과 pathSum를 재귀호출을 적용함으로서 이러한 문제를 해결할 수 있습니다.
pathSum을 재귀로 둠으로서 얻을 수 있는 것들.
- 이 메소드는 트리의 모든 노드를 잠재적인 시작점으로 고려합니다.
- 현재 노드에 대해 checkPathSum을 호출하고, 동시에 왼쪽과 오른쪽 자식 노드에 대해 재귀적으로 pathSum을 호출합니다.
- 이렇게 함으로써 트리의 모든 노드가 경로의 시작점이 될 수 있도록 보장합니다.
이 두 메소드의 조합을 통해:
- 모든 가능한 시작점(모든 노드)이 고려됩니다.
- 각 시작점에서 시작하는 모든 가능한 경로가 계산됩니다.
따라서 이 알고리즘은 문제의 요구사항인 "경로의 시작이 루트일 필요가 없고, 끝이 잎 노드일 필요도 없다"를 완벽하게 만족시킵니다. 모든 노드가 잠재적인 시작점이 되고, 각 시작점에서 모든 가능한 경로를 고려하기 때문입니다.
- Total
- Today
- Yesterday
- 도커
- 정의
- 스케줄러
- Cache
- LocalDate
- 컨테이너
- leatcode
- Linux
- MySQL
- spring
- mybatis
- centos7
- docker
- 권한
- insert
- 이미지
- Java
- dfs
- hazelcast
- 네이버 클라우드
- Quartz
- dockerfile
- 캘린더
- 격리수준
- Lock
- 알고리즘
- 개념 이해하기
- 캐시
- 리눅스
- ncp
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
